Holding edges (bevel) while maintaining quad based geometry
Hello everyone,
this is my first post here, so please bear with me. I am right now trying to add holding edges to my model for subdivision. I'm doing this by beveling the edges and manually cutting the polygons to maintain a quad based geometry. Since my method produces a bunch more edge loops and thus more polygons, I am looking for a smart alternative.
Maybe one of you guys has an idea to go about this.
(The images show how I started.)
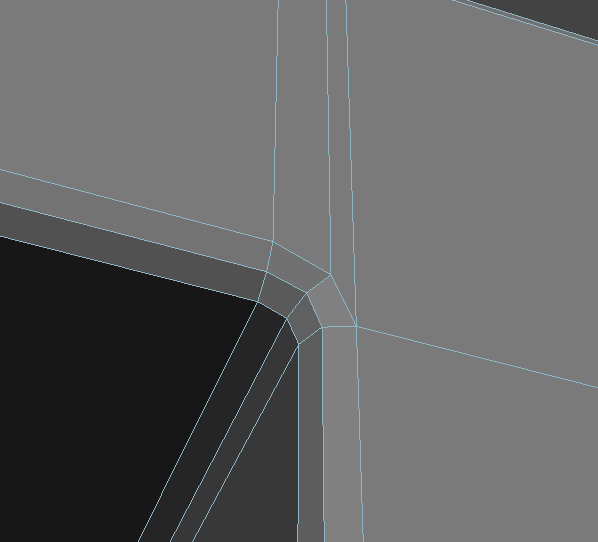

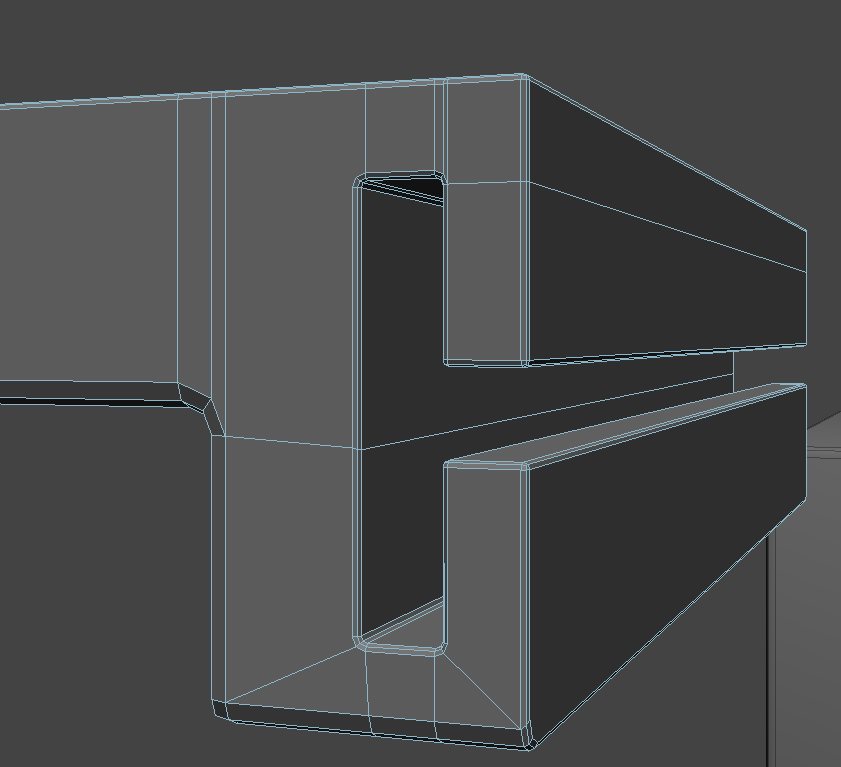
this is my first post here, so please bear with me. I am right now trying to add holding edges to my model for subdivision. I'm doing this by beveling the edges and manually cutting the polygons to maintain a quad based geometry. Since my method produces a bunch more edge loops and thus more polygons, I am looking for a smart alternative.
Maybe one of you guys has an idea to go about this.
(The images show how I started.)



Replies
You'll end up duplicating the mesh and deleting all those support/holding edges as they aren't needed for your in-game mesh.
Something to note is that the N-gons in your model will probably be a bigger problem than any triangles.
And lowpoly geometry is fine to have triangles.
result
smoothed