prolow tools thread

prolow

maya poly rounder
uploaded the uncompiled .py cause I suspect the .pyc was causing incompatibility issues
[ame="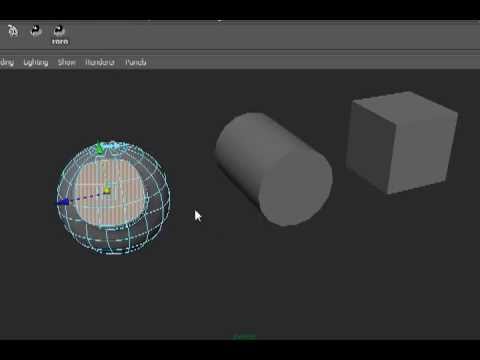http://www.youtube.com/watch?v=YnYU3UUUbIo"]round tool for maya - YouTube[/ame]

BARDLER

Hmm this looks promising. I will try this tomorrow.

St.Sabath

Very nice,testing...!

Xelioth

Thanks for the repost prolow! This version works flawless in 2014.

Deadly Nightshade

I think I like it! Thumbs up!

Joopson

How do you get it to work? I through the script onto a shelf button, but it doesn't seem to do anything.

Xelioth

Joopson wrote: »

How do you get it to work? I through the script onto a shelf button, but it doesn't seem to do anything.

Here's his original post in the What Are You Working On thread. Hopefully this'll get ya.

prolow wrote:

put in C: \Users\*userName\Documents\maya*version\scripts\
reopen maya
enter python command:
import round
select something
round.round()

passerby

@joopson make a shelf button like this!

import round
round.round()

@ prolow you could drastically cut down on the amount of code needed if you would use the point and vector classes from either OpenMaya or from pymel. since that way you would have method available already for adding, subtracting and doing your dot and cross products, and you would have it all implemented with operator overrides.

Joopson

Fanks! Works a charm. Cool script. Probably will prove to be very useful.

prolow

passerby wrote: »

@ prolow you could drastically cut down on the amount of code needed if you would use the point and vector classes from either OpenMaya or from pymel. since that way you would have method available already for adding, subtracting and doing your dot and cross products, and you would have it all implemented with operator overrides.

indeed you are correct sir, I was pretty comfortable with OpenMaya when I wrote this, don't recall why I didn't use a bit of it then:P, think it was mostly copy pasta from some of my older scripts.

54Strat

Looking good.

I've been working on something similiar, and like yourself using a similar algorithm, i.e using the avg centre and re-positioning the vert along a vector from this centre a distance of average radius away and intersecting a normalized plane.

Just wondering, have you looked at forcing the initial border selection to create a regular polygon? I'm halfway though doing this, and the maths is getting a bit heavy. Obviously it would only work well if the selection were coplanar, but it might be useful.

prolow

@54Strat
If I undetsand what your talking about is regularly spaced boarder points. Then yes I thought about it. That was a feature in the XSI version of the tool that I was basing this one one. I stopped b/c as you said it gets hairy. I'm curious about how your trying to do it though. Feel free to mod this one with your solution.

54Strat

Run through the existing algorithm, then get the winding order of the border vertices and choose a likely starting point (orthogonally aligned, symmetry or closest radius or edge, or pre-calc and measure least distortion somehow). Then iterate in winding order, and rotate each vertex about the centre so the angle with the previous vertex is (number of vertices)/360. I'm nearly there, just need to find time to finish it.

I did try by calculating what an edge length should be from a circumscribed regular polygon, this worked but only after executing the whole code multiple times as it got closer and closer to it's target lengths. Once you change one edge length, the whole polygon changes and needs to be re calculated.

Not sure how to deal with plane changes though, maybe do it per plane and fix the points on the intersection. Interesting problem.

passerby

Your tool pops me a division by 0 error if i try and use it on a edge loop around a object.

prolow

@54Strat - I starting thinking about how to choose the starting point...then ma head esplod. You talking about solving it iteratively gets me thinking the best way may be a "peltting" type solution.

@passerby - I should catch the error, but I don't think there's a way for the same function to do both scenarios. This function starts by 'spherizing' the points then projects them back to their original vert normal plane along a vector made of the average vert normals. That projection vector gets f'd when it's the average of vert normals pointing in opposite directions. I think thats the case when you include any points that face >= 180 degrees from each other.
I could however catch the case early and skip the projection, leaving it spherical. What do you think?

passerby

ah, ya that makes perfect sense, ya i would just check to make sure you don't end up with a vector of 0, 0, 0 and ignore the projection if you do, and just spherize.

prolow

update:
- Changed function to skip back projection when appropriate, i.e. - Edge rings round out.
- Recognizes multiple selection sets, i.e. - selecting two unconnected groups of components results in two circles

chriszuko

Very Cool! Will definitely try this out!

xerious3d

sick - will give this a whirl! can't wait. Good job and thanks for sharing!:thumbup:

prolow

got a new one, not for release really, just exploring openGL drawing for tool widgets
[ame="http://www.youtube.com/watch?v=aPgBjNdCD50"]weight tweaker tool - YouTube[/ame]

Visum

That rounding script is pretty awesome. Thx for sharing.

passerby

Looks pretty cool never tried to work with the opengl part of the api yet but would be useful.